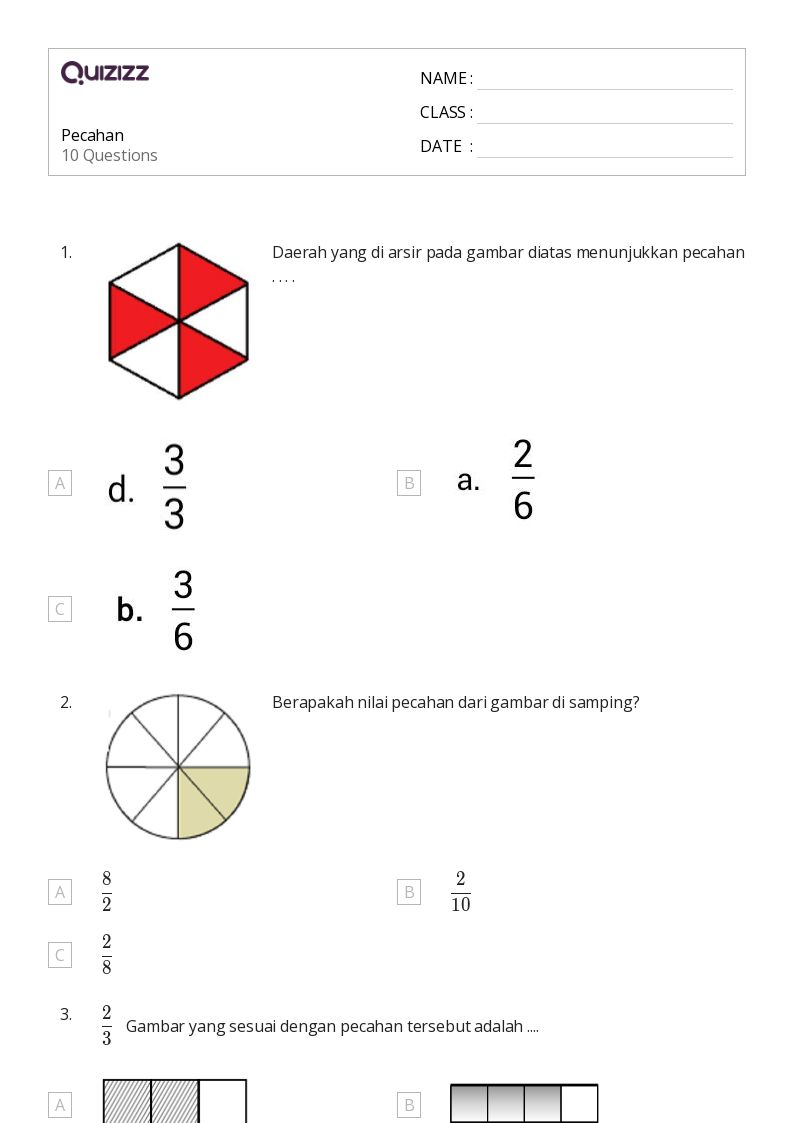
Kisi kisi soal pecahan kelas 4

Membongkar Misteri Pecahan: Panduan Lengkap Kisi-Kisi Soal Matematika Kelas 4

Pecahan seringkali menjadi momok bagi siswa kelas 4. Konsep yang terasa abstrak ini menuntut pemahaman yang mendalam, bukan sekadar hafalan. Agar para siswa dapat menghadapi ujian dan penilaian dengan percaya diri, pemahaman terhadap kisi-kisi soal menjadi kunci utama. Artikel ini akan membongkar seluk-beluk kisi-kisi soal pecahan untuk kelas 4 SD, memberikan gambaran komprehensif tentang materi yang akan diuji, tingkat kesulitan, serta tips jitu untuk menguasainya.

Mengapa Kisi-Kisi Soal Penting?

Bayangkan Anda akan mengikuti sebuah kompetisi, namun tidak tahu cabang olahraganya, peraturan permainannya, atau bahkan target skornya. Tentu Anda akan merasa cemas dan kurang persiapan. Kisi-kisi soal berperan layaknya peta dan kompas dalam ujian. Ia memberikan informasi krusial tentang:

• Materi yang Diujikan: Apa saja topik pecahan yang akan muncul dalam soal.
• Alokasi Bobot Materi: Topik mana yang memiliki porsi lebih besar dalam penilaian.
• Tingkat Kesulitan Soal: Seberapa kompleks soal yang akan dihadapi (mudah, sedang, sulit).
• Jenis Soal: Apakah akan ada soal pilihan ganda, isian singkat, atau uraian.

Dengan memahami kisi-kisi, siswa dapat memfokuskan belajar pada area yang paling relevan, mengalokasikan waktu belajar secara efektif, dan membangun strategi pengerjaan soal yang lebih terarah.

Struktur Umum Kisi-Kisi Soal Pecahan Kelas 4

Kisi-kisi soal pecahan kelas 4 umumnya disusun berdasarkan Standar Kompetensi Lulusan (SKL) dan Kompetensi Dasar (KD) yang telah ditetapkan dalam kurikulum. Materi pecahan di kelas 4 biasanya mencakup beberapa topik utama, yang akan kita bedah satu per satu.

I. Konsep Dasar Pecahan

Ini adalah fondasi dari seluruh pembelajaran pecahan. Soal pada bagian ini bertujuan untuk menguji pemahaman siswa tentang apa itu pecahan, bagaimana merepresentasikannya, dan bagian-bagiannya.

• Materi Pokok:

  • Pengertian Pecahan: Siswa harus memahami bahwa pecahan adalah bagian dari keseluruhan.
  • Penyebut dan Pembilang: Mengenali dan memahami fungsi dari angka yang berada di atas (pembilang) dan di bawah (penyebut) garis pecahan.
  • Representasi Pecahan: Mampu menggambarkan pecahan menggunakan benda konkret (misalnya, memotong pizza, membagi kue), gambar (lingkaran, persegi panjang), atau garis bilangan.
  • Pecahan Sederhana: Memahami pecahan seperti 1/2, 1/3, 1/4, 2/3, 3/4, dll.
  • Pecahan Senilai: Mengenali bahwa pecahan yang berbeda bisa memiliki nilai yang sama (misalnya, 1/2 = 2/4 = 3/6).

• Indikator Soal yang Mungkin Muncul:

  • Siswa dapat mengidentifikasi pecahan yang mewakili bagian yang diarsir dari sebuah bangun datar.
  • Siswa dapat menuliskan pecahan yang sesuai dengan situasi sehari-hari (misalnya, "Adi makan 2 potong dari 8 potong pizza, berapa bagian pizza yang dimakan Adi?").
  • Siswa dapat membandingkan visualisasi pecahan dengan menggunakan gambar atau benda.
  • Siswa dapat menentukan dua atau lebih pecahan yang senilai dengan diberikan salah satunya.

• Tingkat Kesulitan: Umumnya berada pada kategori mudah hingga sedang. Soal-soal ini lebih mengedepankan pemahaman konseptual dan visualisasi.

II. Operasi Dasar pada Pecahan

Setelah memahami konsep dasar, siswa akan diperkenalkan dengan operasi-operasi aritmetika pada pecahan.

• Materi Pokok:

  • Penjumlahan Pecahan:
    • Penjumlahan pecahan berpenyebut sama.
    • Penjumlahan pecahan berpenyebut berbeda (menggunakan konsep KPK untuk menyamakan penyebut).
  • Pengurangan Pecahan:
    • Pengurangan pecahan berpenyebut sama.
    • Pengurangan pecahan berpenyebut berbeda (menggunakan konsep KPK untuk menyamakan penyebut).
  • Perkalian Pecahan:
    • Perkalian pecahan biasa dengan bilangan bulat.
    • Perkalian dua pecahan biasa.
  • Pembagian Pecahan:
    • Pembagian pecahan biasa dengan bilangan bulat.
    • Pembagian bilangan bulat dengan pecahan biasa.

• Indikator Soal yang Mungkin Muncul:

  • Siswa dapat menghitung hasil penjumlahan dua pecahan berpenyebut sama.
  • Siswa dapat menyelesaikan soal cerita yang melibatkan penjumlahan pecahan berpenyebut berbeda.
  • Siswa dapat menentukan hasil pengurangan dua pecahan berpenyebut sama.
  • Siswa dapat menjawab soal pengurangan pecahan berpenyebut berbeda dalam konteks masalah.
  • Siswa dapat menghitung hasil perkalian pecahan biasa dengan bilangan bulat.
  • Siswa dapat menghitung hasil perkalian dua pecahan biasa.
  • Siswa dapat menyelesaikan soal yang melibatkan pembagian pecahan sederhana.

• Tingkat Kesulitan: Mulai dari sedang hingga sulit, terutama untuk operasi penjumlahan dan pengurangan dengan penyebut berbeda yang memerlukan pemahaman KPK. Perkalian dan pembagian juga memerlukan pemahaman konsep yang kuat.

III. Pecahan Campuran dan Pecahan Tak Wajar

Topik ini memperluas pemahaman siswa tentang bentuk-bentuk pecahan.

• Materi Pokok:

  • Mengubah Pecahan Tak Wajar menjadi Pecahan Campuran: Memahami bahwa pecahan tak wajar (pembilang lebih besar dari penyebut) dapat dinyatakan dalam bentuk bilangan bulat dan pecahan biasa.
  • Mengubah Pecahan Campuran menjadi Pecahan Tak Wajar: Memahami kebalikan dari proses di atas.
  • Operasi Hitung pada Pecahan Campuran dan Pecahan Tak Wajar: Melibatkan penjumlahan, pengurangan, perkalian, dan pembagian yang melibatkan bentuk-bentuk pecahan ini.

• Indikator Soal yang Mungkin Muncul:

  • Siswa dapat mengubah pecahan tak wajar seperti 7/3 menjadi pecahan campuran 2 1/3.
  • Siswa dapat mengubah pecahan campuran seperti 3 1/2 menjadi pecahan tak wajar 7/2.
  • Siswa dapat menyelesaikan soal penjumlahan atau pengurangan yang melibatkan pecahan campuran.
  • Siswa dapat menghitung hasil perkalian atau pembagian yang melibatkan pecahan tak wajar.

• Tingkat Kesulitan: Cenderung sedang hingga sulit, karena memerlukan kemampuan mengubah bentuk pecahan sebelum melakukan operasi hitung.

IV. Perbandingan Pecahan

Mampu membandingkan dua atau lebih pecahan adalah keterampilan penting.

• Materi Pokok:

  • Membandingkan Pecahan dengan Penyebut Sama: Relatif mudah, cukup membandingkan pembilangnya.
  • Membandingkan Pecahan dengan Penyebut Berbeda: Memerlukan penyamaan penyebut terlebih dahulu atau menggunakan konsep garis bilangan.
  • Mengurutkan Pecahan: Menata pecahan dari yang terkecil ke terbesar atau sebaliknya.

• Indikator Soal yang Mungkin Muncul:

  • Siswa dapat menentukan pecahan mana yang lebih besar antara 3/5 dan 4/5.
  • Siswa dapat membandingkan dua pecahan dengan penyebut berbeda menggunakan tanda <, >, atau =.
  • Siswa dapat mengurutkan tiga atau lebih pecahan dari yang terkecil ke terbesar.

• Tingkat Kesulitan: Sedang, terutama ketika harus membandingkan pecahan dengan penyebut berbeda yang memerlukan penyamaan penyebut.

V. Soal Cerita dan Aplikasi Pecahan

Bagian ini menguji kemampuan siswa dalam menerapkan konsep pecahan dalam kehidupan sehari-hari.

• Materi Pokok:

  • Semua operasi hitung dan konsep pecahan diterapkan dalam konteks masalah praktis.
  • Contoh: masalah takaran, pembagian kue, waktu, jarak, dll.

• Indikator Soal yang Mungkin Muncul:

  • Soal cerita yang melibatkan penjumlahan atau pengurangan bahan-bahan dalam resep masakan.
  • Soal cerita tentang pembagian benda (misalnya, pita, uang) kepada beberapa orang.
  • Soal cerita yang memerlukan pemahaman pecahan untuk menghitung sisa atau bagian yang sudah digunakan.

• Tingkat Kesulitan: Sedang hingga sulit, karena siswa tidak hanya harus menguasai operasi hitung, tetapi juga mampu menganalisis masalah, mengidentifikasi informasi yang relevan, dan menerjemahkannya ke dalam bentuk operasi pecahan.

Tips Jitu Menguasai Materi Pecahan Kelas 4 Berdasarkan Kisi-Kisi:

1. Pahami Konsep Dasar dengan Visualisasi: Jangan hanya menghafal rumus. Gunakan benda konkret, gambar, atau garis bilangan untuk memahami makna pembilang dan penyebut, serta representasi pecahan.
2. Latihan Soal Berulang: Kerjakan berbagai macam soal dari setiap topik yang ada di kisi-kisi. Semakin sering berlatih, semakin terbiasa siswa dengan pola soal dan cara penyelesaiannya.
3. Fokus pada Penyamaan Penyebut: Penjumlahan dan pengurangan pecahan berpenyebut berbeda adalah kunci. Kuasai konsep KPK (Kelipatan Persekutuan Terkecil) dengan baik. Latihan soal yang banyak untuk bagian ini.
4. Ubah Bentuk Pecahan dengan Mahir: Latihan mengubah pecahan tak wajar ke campuran dan sebaliknya secara rutin. Ini akan sangat membantu dalam menyelesaikan soal-soal yang lebih kompleks.
5. Jangan Takut Soal Cerita: Baca soal cerita dengan cermat. Identifikasi informasi penting, tentukan operasi hitung yang tepat, lalu selesaikan. Buatlah ilustrasi sederhana jika perlu.
6. Review Materi Secara Berkala: Jangan menunda belajar hingga mendekati ujian. Lakukan review materi secara berkala agar pemahaman tetap segar.
7. Manfaatkan Sumber Belajar: Gunakan buku teks, buku latihan, video pembelajaran, atau aplikasi edukatif yang membahas pecahan.
8. Diskusi dengan Teman atau Guru: Jika ada materi yang sulit dipahami, jangan ragu untuk bertanya kepada guru atau berdiskusi dengan teman. Penjelasan dari orang lain terkadang bisa membuka sudut pandang baru.
9. Perhatikan Tingkat Kesulitan: Saat berlatih, bedakan soal yang mudah, sedang, dan sulit. Kuasai dulu yang mudah, lalu bertahap ke yang lebih sulit.

Contoh Alokasi Bobot dalam Kisi-Kisi (Ilustrasi):

Sebuah kisi-kisi yang ideal akan memberikan gambaran persentase atau jumlah soal untuk setiap topik. Misalnya:

• Konsep Dasar Pecahan: 20%
• Operasi Dasar (Penjumlahan & Pengurangan): 30%
• Operasi Dasar (Perkalian & Pembagian): 20%
• Pecahan Campuran & Tak Wajar: 15%
• Perbandingan & Urutan Pecahan: 10%
• Soal Cerita: 5% (Ini bisa saja terintegrasi di setiap topik operasi)

Catatan: Alokasi bobot ini hanya ilustrasi. Bentuk dan isi kisi-kisi yang sebenarnya dapat bervariasi tergantung sekolah dan penyusun soal.

Penutup

Mempelajari pecahan di kelas 4 memang menantang, namun dengan pemahaman yang tepat tentang kisi-kisi soal, siswa dapat mempersiapkan diri secara optimal. Fokus pada konsep dasar, latihan yang konsisten, dan strategi belajar yang terarah akan menjadikan pecahan bukan lagi sebagai momok, melainkan sebagai salah satu materi matematika yang menyenangkan dan bermanfaat. Dengan bekal pemahaman kisi-kisi ini, semoga para siswa kelas 4 dapat meraih hasil terbaik dalam setiap penilaian matematika mereka.

>